Example of Lecture 14, 15 – ARIMA for time series#
Example from: https://www.projectpro.io/article/how-to-build-arima-model-in-python/544
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
df = pd.read_csv('WWWusage.csv', names = ['index','time','value'], header = 0)
print(f"Total samples are: {len(df)}")
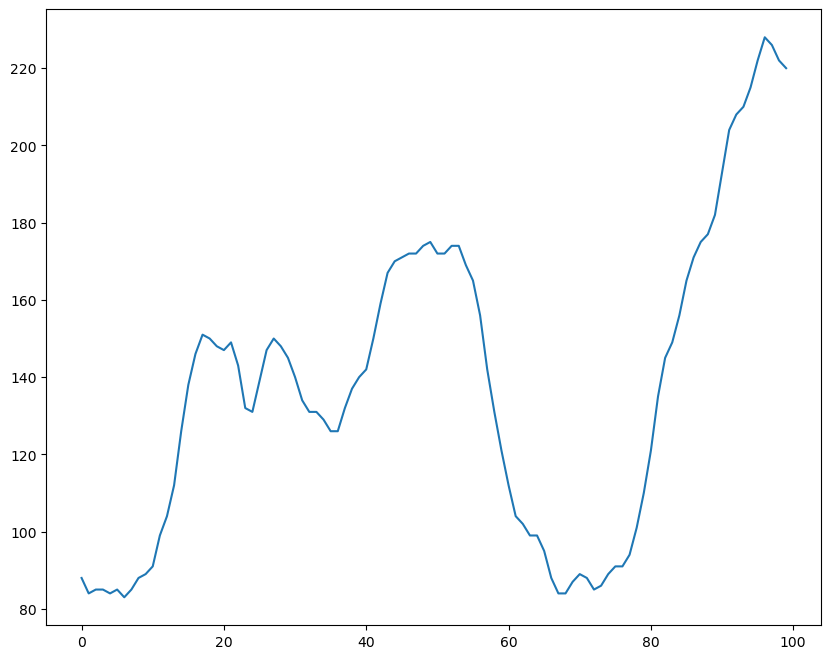
fig = plt.figure(figsize = (10, 8))
ax = fig.add_subplot(1,1,1)
ax.plot(df['value'])
plt.show()
Total samples are: 100
ARIMA(p,d,q)#
p: order of autocorrection
d: order of differential
q: order of moving average
The key to build a ARIMA model is to choose proper p, d, q
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(df.value)
plt.show()
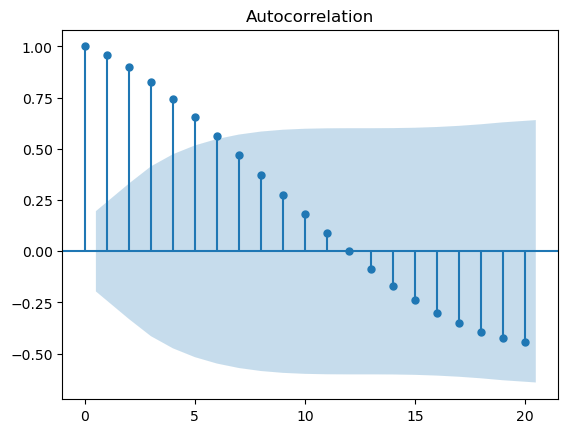
Clearly, the data is not ideal for the ARIMA model to directly start autoregressive training. So let’s see how the differencing segment of ARIMA makes the data stationary.
f = plt.figure(figsize = (12, 5))
ax1 = f.add_subplot(121)
ax1.set_title("1st order differencing")
ax1.plot(df.value.diff())
ax2 = f.add_subplot(122)
plot_acf(df.value.diff().dropna(),ax=ax2)
plt.show()
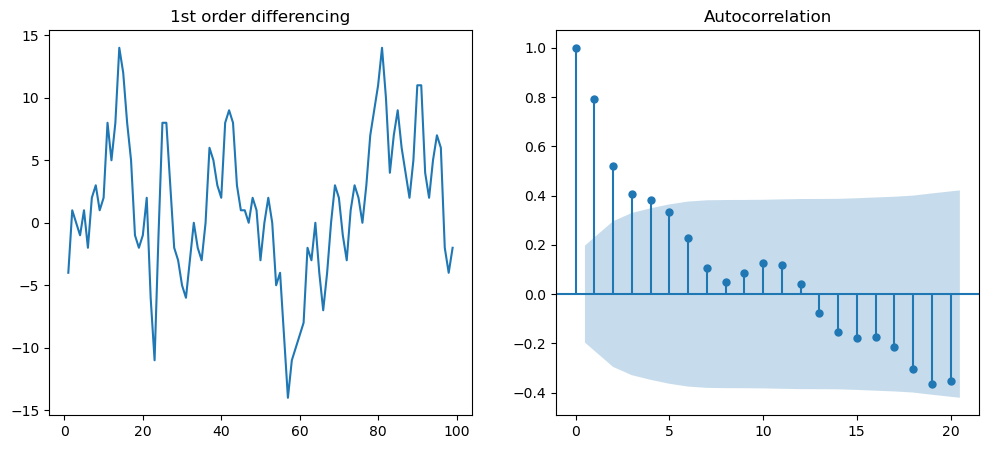
As seen above, first-order differencing shakes up autocorrelation considerably. We can also try 2nd order differencing to enhance the stationary nature.
# In the following, we will do for second differencing
f = plt.figure(figsize = (12, 5))
ax1 = f.add_subplot(121)
ax1.set_title('2nd differencing')
ax1.plot(df.value.diff().diff())
ax2 = f.add_subplot(122)
plot_acf(df.value.diff().diff().dropna(),ax=ax2)
plt.show()
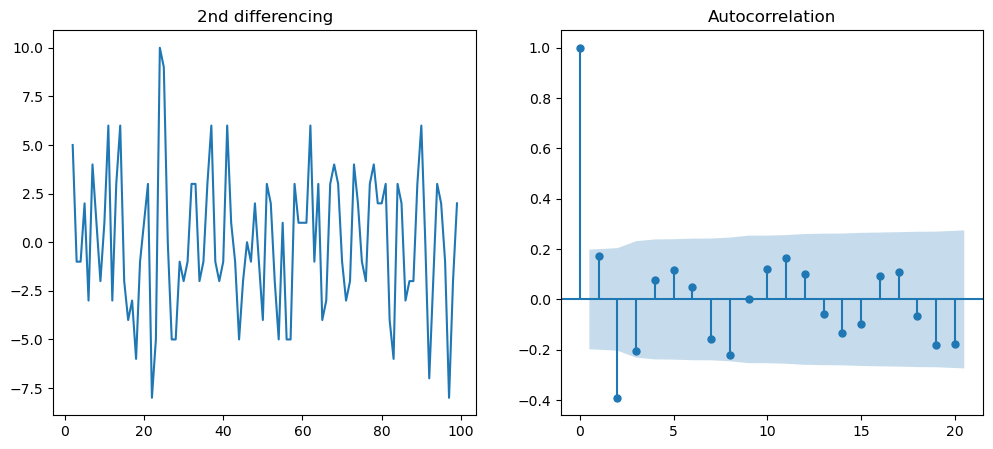
# Non stationary test by ADF test
from statsmodels.tsa.stattools import adfuller
result = adfuller(df.value.dropna())
print('p-value: ', result[1])
result = adfuller(df.value.diff().dropna())
print('p-value: ', result[1])
result = adfuller(df.value.diff().diff().dropna())
print('p-value: ', result[1])
p-value: 0.12441935447109487
p-value: 0.07026846015272728
p-value: 2.843428755547158e-17
# Next we can determine the value of "p" for first differencing
f = plt.figure(figsize=(12,5))
ax1 = f.add_subplot(121)
ax1.set_title('First order differencing')
ax1.plot(df.value.diff().dropna())
ax2 = f.add_subplot(122)
plot_pacf(df.value.diff().dropna(), ax=ax2)
plt.show()
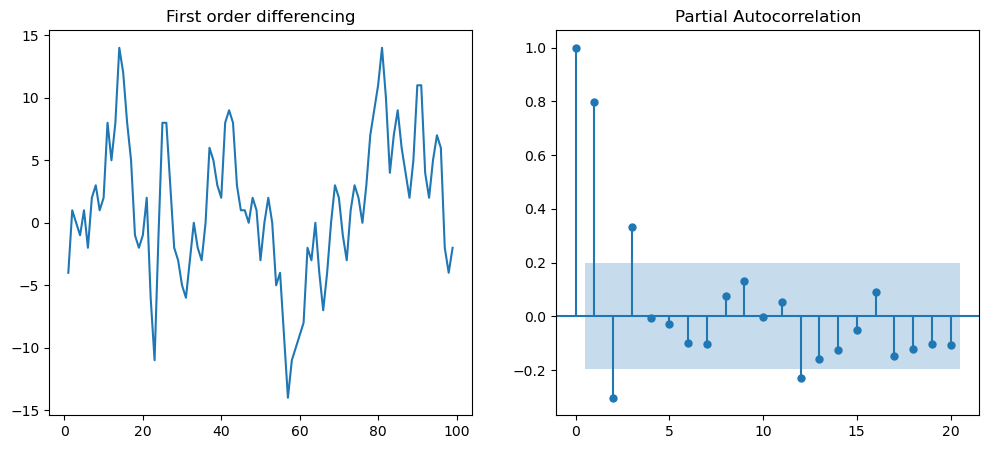
# Next we can determine the value of "p" for second differencing
f = plt.figure(figsize=(12,5))
ax1 = f.add_subplot(121)
ax1.set_title('First order differencing')
ax1.plot(df.value.diff().diff().dropna())
ax2 = f.add_subplot(122)
plot_pacf(df.value.diff().diff().dropna(), ax=ax2)
plt.show()
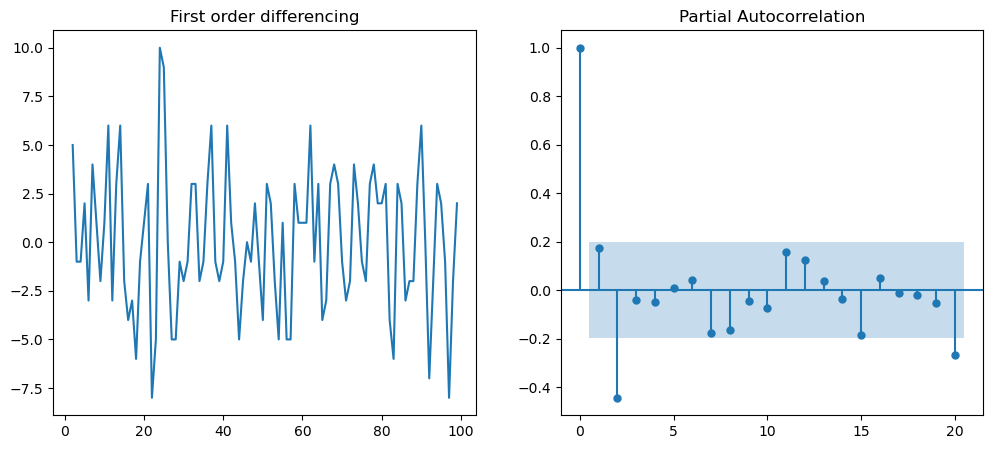
Thus, final ARIMA model defined as ARIMA(p=1, d=1,q= 2).#
PART II: Fit the ARIMA model#
from statsmodels.tsa.arima.model import ARIMA
arima_model = ARIMA(df.value, order = (1,1,2))
model = arima_model.fit()
print(model.summary())
SARIMAX Results
==============================================================================
Dep. Variable: value No. Observations: 100
Model: ARIMA(1, 1, 2) Log Likelihood -254.126
Date: Fri, 20 Jan 2023 AIC 516.253
Time: 18:47:18 BIC 526.633
Sample: 0 HQIC 520.453
- 100
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.6976 0.130 5.365 0.000 0.443 0.952
ma.L1 0.4551 0.169 2.699 0.007 0.125 0.786
ma.L2 -0.0664 0.157 -0.424 0.671 -0.373 0.241
sigma2 9.7898 1.421 6.889 0.000 7.005 12.575
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.09
Prob(Q): 0.98 Prob(JB): 0.95
Heteroskedasticity (H): 0.63 Skew: -0.07
Prob(H) (two-sided): 0.19 Kurtosis: 3.03
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
# test another setting of (p, d,q)
arima_model = ARIMA(df.value, order = (1,2,2))
model = arima_model.fit()
print(model.summary())
SARIMAX Results
==============================================================================
Dep. Variable: value No. Observations: 100
Model: ARIMA(1, 2, 2) Log Likelihood -252.594
Date: Fri, 20 Jan 2023 AIC 513.189
Time: 18:48:28 BIC 523.529
Sample: 0 HQIC 517.371
- 100
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.6530 0.103 6.359 0.000 0.452 0.854
ma.L1 -0.4743 2.191 -0.217 0.829 -4.768 3.819
ma.L2 -0.5251 1.130 -0.465 0.642 -2.740 1.689
sigma2 9.8299 21.283 0.462 0.644 -31.884 51.544
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.22
Prob(Q): 0.95 Prob(JB): 0.90
Heteroskedasticity (H): 0.61 Skew: -0.11
Prob(H) (two-sided): 0.16 Kurtosis: 3.08
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
model.plot_predict(dynamic=False)
plt.show()
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_26020\2666529794.py in <cell line: 1>()
----> 1 model.plot_predict(dynamic=False)
2 plt.show()
~\Anaconda3\lib\site-packages\statsmodels\base\wrapper.py in __getattribute__(self, attr)
32 pass
33
---> 34 obj = getattr(results, attr)
35 data = results.model.data
36 how = self._wrap_attrs.get(attr)
AttributeError: 'ARIMAResults' object has no attribute 'plot_predict'
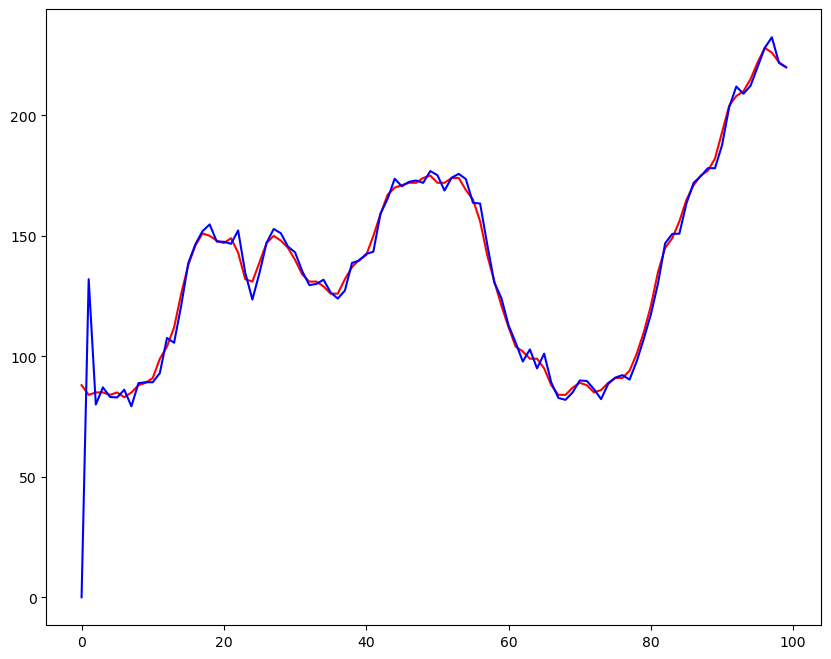
plt.figure(figsize = (10,8))
plt.plot(df.value, color = 'r')
plt.plot(model.predict(),color = 'b')
plt.show()
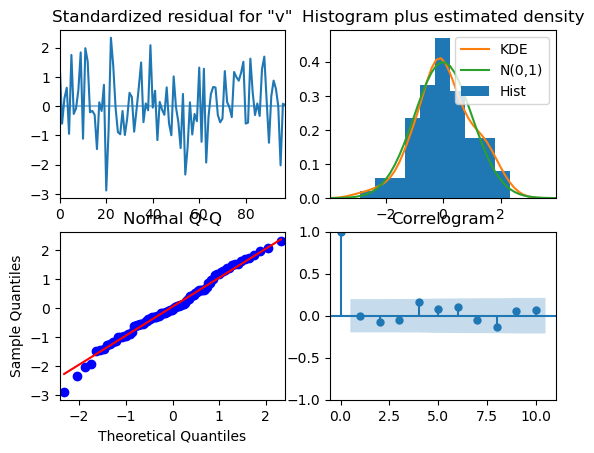
model.plot_diagnostics()